
It didn't look as neat as the previous solution, but it does show us that there is more than one way to set up and solve matrix equations. In fact it is just like the Inverse we got before, but Transposed (rows and columns swapped over). Then (also shown on the Inverse of a Matrix page) the solution is this:

Similarly, solutions to systems of linear equations in three unknowns Recall from Unit LA1, Subsection 1. The rows and columns have to be switched over ("transposed"): The solution to a system of simultaneous linear equations in two unknowns (xand y) corresponds to the points of intersection (if any) of lines in R2. I want to show you this way, because many people think the solution above is so neat it must be the only way.Īnd because of the way that matrices are multiplied we need to set up the matrices differently now. Quite neat and elegant, and the human does the thinking while the computer does the calculating.įor fun (and to help you learn), let us do this all again, but put matrix "X" first. Just like on the Systems of Linear Equations page. Then multiply A -1 by B (we can use the Matrix Calculator again): (I left the 1/determinant outside the matrix to make the numbers simpler) It means that we can find the values of x, y and z (the X matrix) by multiplying the inverse of the A matrix by the B matrix.įirst, we need to find the inverse of the A matrix (assuming it exists!) Then (as shown on the Inverse of a Matrix page) the solution is this: A is the 3x3 matrix of x, y and z coefficients.Which is the original left side of our equations above (you might like to check that). Sometimes, a homogeneous system has non-zero vectors also to be solutions, To find them, we have to use the matrices and the elementary row operations.Why does go there? Because when we Multiply Matrices the left side becomes: For example, (x, y) = (0, 0) is a solution of the homogeneous system x + y = 0, 2x - y = 0. What is the Solution of Homogeneous System of Linear Equations?Ī zero vector is always a solution to any homogeneous system of linear equations. If each equation in it has its constant term to be zero, then the system is said to be homogeneous. How do You Know if a System of Equations is Homogeneous?Ī system has two or more equations in it. Any other solution than the trivial solution (if any) is called a nontrivial solution.
What are Trivial and Nontrivial Solutions of a Homogeneous System of Linear Equations?Ī vector formed by all zeros (zero vector) is always a solution of any homogeneous linear system and it is called a trivial solution. Now let us the expand the first two rows as equations:Īnswer: The solution is (x, y, z) = (-t, -2t, t), where 't' is a real number.įAQs on Homogeneous System of Linear Equations What is a Homogeneous Linear Equation Example?Ī homogeneous linear equation is a linear equation in which the constant term is 0. Let us find them using the elementary row operations on the coefficient matrix.ĭividing the 2 nd row by 51 and and 3 rd row by 17, Therefore, the system has an infinite number of solutions (along with the trivial solution (x, y, z) = (0, 0, 0)). Let us find the determinant of the coefficient matrix: When t = 0.5: (x, y, z) = (-1, 0.5, 0.5), etcĮxample 3: How many solutions does the following system has? Find them all. For example, some nontrivial solutions of the above homogeneous system can be: Thus, the solution is (x, y, z) = (-2t, t, t) which represents an infinite number of nontrivial solutions as 't' can be replaced with one of the real numbers (which is an infinite set). Hence we should assume one of the variables to be a parameter (say t which is a real number). We have two equations in three variables. Just expand the first two rows of the above matrix as equations. It means that the system has nontrivial solutions also. We couldn't convert it into the upper diagonal matrix as we ended up with a row of zeros in the matrix.
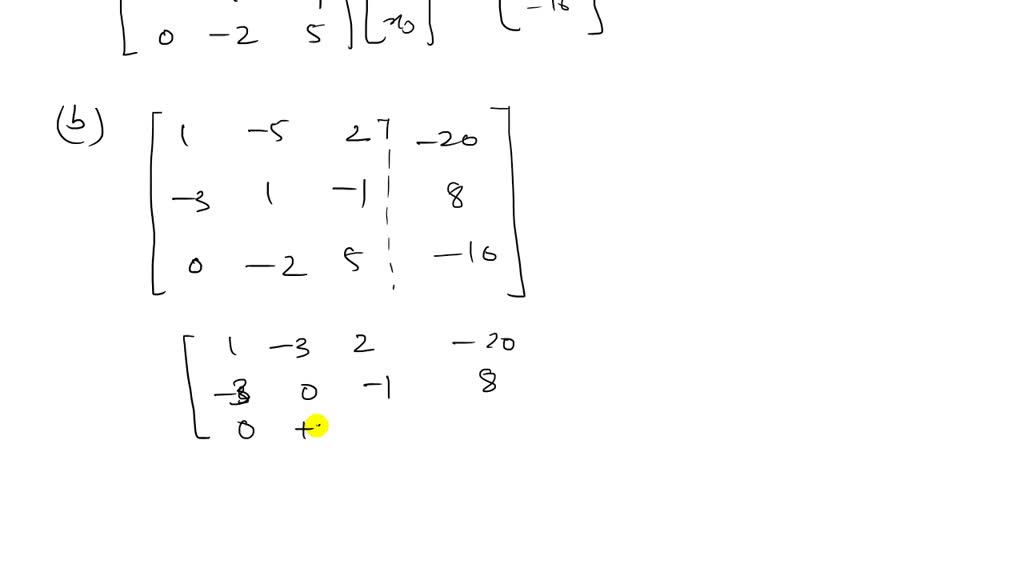
Let us take the coefficient matrix of the above system and apply row operations in order to convert it into an upper diagonal matrix. We can find them using the matrix method and applying row operations. But it may (or may not) have other solutions than the trivial solutions that are called nontrivial solutions. For example, the system formed by three equations x + y + z = 0, y - z = 0, and x + 2y = 0 has the trivial solution (x, y, z) = (0, 0, 0). , 0) is obviously a solution to the system and is called the trivial solution (the most obvious solution). Since there is no constant term present in the homogeneous systems, (x₁, x₂. Solving Homogeneous System of Linear EquationsĪ homogeneous system may have two types of solutions: trivial solutions and nontrivial solutions.


 0 kommentar(er)
0 kommentar(er)
